This is the fifth in a series of blog posts explaining the usage of the Lindenmayer System Explorer. Clicking on an image will take you to the explorer page, pre-configured to draw that image.

So far, we have seen many different patterns created with the L-system explorer – fractals, dragon curves, snowflakes, and so on. They all have one thing in common: they are made up of a single line.

To create branches, enclose the rules for a branch in square brackets, like so:

[F]+[F]+[F]

Instead of yielding a bent line, it creates a pattern like this:

Not terribly interesting yet, but it does allow for the creation of more interesting shapes. Remember: Astrid Lindenmayer was a botanist, and he originally created this system to model the structure of living plants. If we nest a few brackets, and play around with the angles, we can get patterns like this:

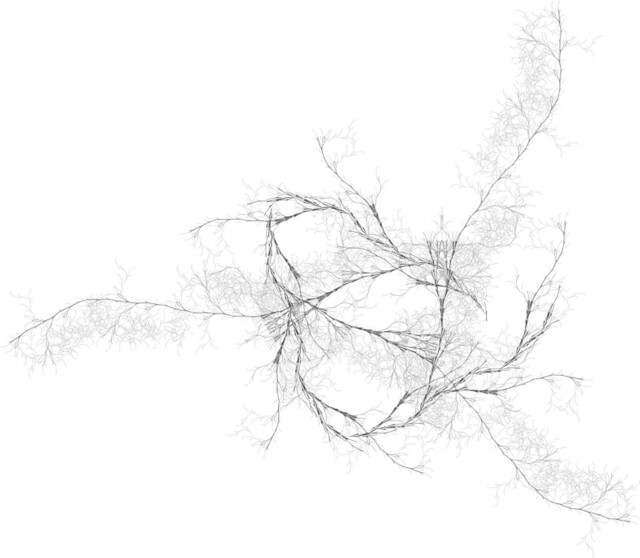
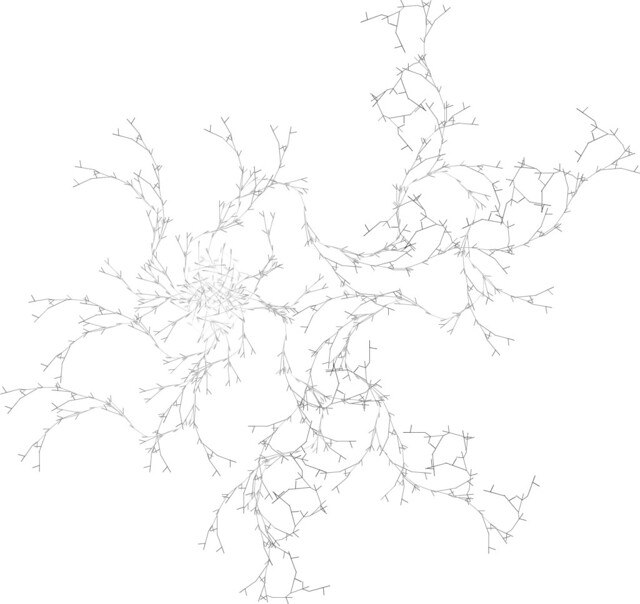
Branch rules can be nested within each other, to the extent that extremely complex patterns can emerge very quickly:

And with a little practice, the patterns can become increasingly plant-like:

So that’s it for branches. In the next post I will show how you can use branching to change the drawing angles, colors, line length and line thickness to create increasingly life-like plants.

More posts on this subject:

Lines
Angles
Rule sets
The Start Condition

In this post I will discuss some of the different patterns created by modifying the start condition in the Lindenmayer System Explorer. Clicking on any of the images will take you to the explorer tool, preloaded with the variables necessary to re-create that image.

So by now you all have seen the basic pattern which is created by the default settings in the explorer:

All well and good, but it feels incomplete; maybe a little lop-sided. Change the start condition to “F+F+F+F”, and you will see this:

How did this happen?!? Look at the angle: 90°. When you click the render button, the start condition and the grammar are run through an algorithm which creates a long string of characters. Every time an “F” is encountered, a line segment is created. Every time a “+” or “-” is encountered, the angle at which the next segment will be drawn is updated by the value in the “angle” field. “+” turns clockwise, “-” turns widdershins. So in this instance, every “+” means the next line will be drawn at a 90° angle to the previous segment. In the first example, having “F” as the starting condition drew, overall, a single quarter of a square pattern. Changing the start condition to “F+F+F+F” means that the initial 90° angle would be repeated 4 times, each at a 90° offset from the previous. 90 x 4 = 360°, which brings the line back to the start position.

This will work with any number which divides evenly into 360. Here is a 5-sided (72°) figure:

Six sides at 60°:

…and so on. As long as the starting condition and angles are correct, you can put almost anything in the grammar and use any number of iterations, and the result will still be a closed shape. Here are a few more:

In the Lindenmayer System Explorer tutorials I am posting I continually refer to “rule sets”, which are the DNA (so to speak) of the shapes which are created when the you click the “RENDER” button.

Rule sets are built as follows:
1. look at the current rule set, which in this instance is equal to the start condition “F”.
2. Look at the grammar, which in this instance is “F:F+F-F-F+F”.
3. Match the grammar character to the left of the colon to the characters in the start condition. Each time you encounter an “F” in the start condition, replace it with everything to the right of the colon in the grammar.
4. If we have not yet done this as many times as the iterator calls for, go back to (1) and repeat it with the updated rule set.

So with the default start condition and grammar, and the iterations set to “1”, the resulting rule set looks like this:

F+F-F-F+F

The Explorer simply replaced all of the “F” characters in the start condition with the entire grammar. Simple enough.

Now change the iterations to “2”, and click “RENDER“. The rule set now looks like this:

F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F

Instead of 9 characters, the rule set is now 49 characters long, and the resulting shape is more complex.

Changing the iterations to 3 will give you this 249-character long rule set:

F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+
F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-
F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-
F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+
F+F-F-F+F

…and here is 4 iterations, for a total of 1249 characters:

F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F

In each of these, the drawing tool starts at the first character and goes through until it reaches the end, following each instruction in order. So the first few characters in the above string would be read as:

“Draw a line. Turn right. Draw a line. Turn left. Draw a line. Turn left. Draw a line. Turn right. Draw a line. Turn right. Draw a line. Turn right.”

This can continue indefinitely. Complex starting conditions, combined with complex grammars and large numbers of iterations, can easily result in rule sets hundreds of millions of characters long.

After lines, angles are the most important in the creation of patterns in an L system. The following are a few examples of what differences in angles look like, based on the default state of the Explorer.

In all of these examples, clicking on the associated image will take you to the explorer, pre-configured to generate that image.

This is the initial condition, with an angle between lines of 90°:

Changing the angle to 60° results in this:

…And here is 45°:

Increasing past 90° makes the pattern more compact. Setting the angle to 120° creates a triangle pattern:

Increasing the iterations with the 120° pattern results in larger sets of nested triangles:

And finally, increasing the angle to 270° effective creates a mirror image of a pattern created with a 90° angle:

These should give you enough starting points to begin creating some interesting patterns. The angles which don’t precisely divide into 360 can result in some interesting interference patterns in the overlapping lines.

This post is meant to provide some basic instructions and simple starting points for using the Lindenmayer System Explorer. Most of what is written here can also be used in other such tools.

Clicking on an image will open the L-System Explorer pre-loaded with the rules set which created that image.

At its simplest, a Lindenmayer system can be used to generate a line.

Play around with line length, iterations, and the number of “F”s in the Start Condition and the Grammar. You should end up with straight lines of varying lengths

Seems like a lot of work just to draw a straight line. Now add a “+” to the Grammar, changing it to this: F:F+FF

Assuming you have not changed any of the other values, you should have a shape which looks like this:

When going through the rule set, every time a “+” is encountered, the drawing tool changes the angle of the next line by the value in the “Angle” field.

Now add a “-” (minus sign) to the Grammar, changing it to this: F:F+F-F. This should give you a much more complex line which looks like this:

Now change the grammar so that it looks like this: F:F+F-F-F+F. Assuming you haven’t changed any of the other values, you see this pattern:

Adjust the Iterations for this one and you will see how a few simple rules can rapidly generate remarkably complex patterns. Here is the previous rule set with four iterations…

…and with five iterations.

Patterns created using the Lindenmayer System Explorer are now bookmark-able and sharable. Click here to see how I created the image at the top of this post.

Building on my Lindenmayer System experiment from a few days ago, here are a few pieces created with the next generation of the tool, which I will be uploading in a few days. Enjoy!